Pythagorean Theorem Project

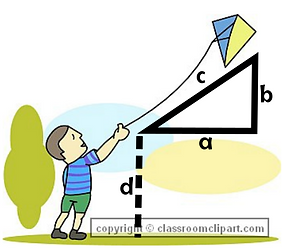
A 4 foot tall boy is flying a kite with a string that extends 50 feet long.  Assume that he holds the kite string even with the top of his head.  A 35 foot tall tree is in the distance, 40 feet away from the boy.  Will the kite be able to soar over the tree or will it get tangled in the branches?

 

Answer:

a = 40 feet, c = 50 feet.  Using Pythagorean Theorem, b = 30 feet.  However, that distance is 30 feet above the boy's head.  The boy is 4 feet tall, so the kite is sailing at 34 feet above the ground.  The kite WILL get tangled with the 35 foot tall tree.

A fire truck has a length of 48 feet and a ladder that extends 75 feet.  The ladder is connected to the top of a 10 foot truck.   Assume each level of the pictured building is 15 feet tall.  Will the ladder be able to extend the entire way to reach the level that is on fire?  Explain your answer.

 

Answer:

If students simply plug in the numbers, a = 48 feet, c = 75 feet, they will find that b = 57.6 feet.  Adding the height of the truck (10 feet), they might say that the ladder will reach 67.6 feet high which is not high enough to reach the building.  However, problem solving students should realize that moving the truck will help the ladder reach higher.
 

Working backwards: The ladder needs to reach to 75 feet at the bottom of the fire.  The truck is already adding 10 feet to the height.  Therefore, b must be more than 65 feet.  Set b = 65 feet. We know the ladder is 75 feet.  Therefore, c = 75 feet.  Using the Pythagorean Theorem to solve for a, a = 37.4 feet.  Our truck is 48 feet long, so if it pulls up next to the building so that 37.4 feet of the truck are sticking out (in other words, 48 - 37.4 = 10.6 feet of the truck overlap with the building), then the ladder WILL be able to reach the fire.